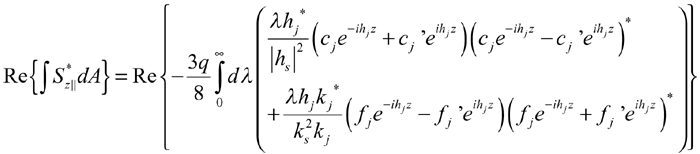Research
Optical Models of Organic Light Emitting Devices
K. Celebi, and T.D. Heidel, M.A. Baldo
Sponsorship: DARPA, NSF
Organic semiconductors are typically characterized by strong optical absorption but relatively poor charge transport. Taken together, these properties oblige the use of thin organic device structures, typically on the order of the wavelength of visible light. Thus, the design of organic photovoltaics (OPVs) and light emitting devices (OLEDs) must consider near field phenomena and the photonic mode density. The traditional approach relies on the dipole model of Chance, Prock and Silbey (CPS).[1] In CPS theory an exciton within the organic device is modeled as a point dipole whose electric field is described by dyadic Green’s functions. This technique calculates the dipole lifetime and the wavevector distribution of its decay. But energy transfer between layers in the stack can only be determined qualitatively by analyzing the wavevector distribution. In many cases, this prevents a quantitative understanding of energy transfer in the multilayer stack. Thus, it is common to couple the exact CPS model with an approximate quantum mechanical model that compares the probability of exciton decay to the various non-radiative and radiative modes of the multilayer stack. Unfortunately, such hybrid approaches suffer from complexity and a lack of accuracy.
We have developed a novel technique that eliminates the need for the quantum mechanical appendage to CPS by analytically determining the Poynting vector.[2] The solution is exact and easily implemented in existing CPS models. Briefly, our analytic work has concluded that the flux through an interface is given by the following two equations for dipoles oriented perpendicular and parallel to the interfaces, respectively; i.e.
, where q is the free space photoluminescent efficiency of the exciton, j is the layer index, λ and h are the amplitudes of the parallel and perpendicular components with respect to the surface of the propagation vector k, and subscript s signifies the source layer. The coefficients c, f and c’ , and f’ are the weighting factors for the left and right traveling eigenfunctions of the Green’s function in cylindrical coordinates.
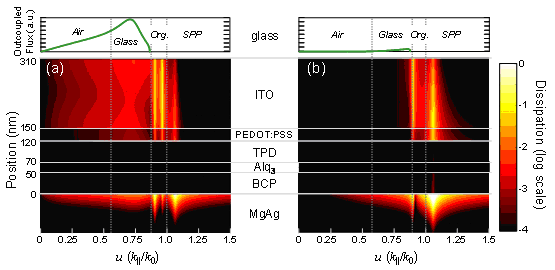
We have applied this approach to a previous experimental measurement of an OLED outcoupling by Segal et al. [3] The model predictions agree with the experiment, yielding a similar outcoupling efficiency and in addition shows the mode-resolved spatial dipole energy dissipation of the same device (Figure 1). Surface-parallel oriented dipoles generate most of the emitted light, and the main optical loss mechanisms are the waveguiding in the glass and organic layers, along with a smaller loss to the plasmon modes of the cathode. Our method can be used for designing low-loss OLED structures and efficient cavity designs.
Figure 1: (a) Absorption of the parallel dipole energy as a function of the position and normalized surface-parallel wavevector. The dipole is located at the middle of the Alq3 layer and the emission wavelength is λ = 535 nm. Bright features correspond to a higher absorption. The green curve shows the outcoupled energy flux. (b) Same absorption as in part (a) but for perpendicular dipole. Perpendicular dashed lines divide this flux into air-outcoupled, glass-waveguided, organics-waveguided and surface plasmon polariton (SPP) portions. At λ = 535 nm, the dielectric constants for Mg, BCP, Alq3, TPD, PEDOT and ITO are the following: ε = 1.908 + 0.265i, ε = 2.985 + (4.11×10-5)i, ε = 2.962, ε = 2.985 + (4.11×10-5)i, ε = 2.304 + (3.33×10-2)i and ε = 3.295 + (3.63×10-2)i, respectively. Note that the dielectric constant of TPD was assumed to be equal that of BCP. (Figure is taken from [2]).
This technique is also useful for calculating energy transfer within an organic device. We have used it extensively to predict the surface plasmon mediated energy transfer efficiency in photovoltaic cells with external antennas.
Matlab code for model: Dipole Code
Relevant Publications
- R.R. Chance, A. Prock and R. Silbey, “Molecular fluorescence and energy transfer near metal interfaces,” in Advances in Chemical Physics Vol. 37, I. Prigogine and S. A. Rice, Eds. New York: Wiley, 1978.
- K. Celebi, T.D. Heidel, and M.A. Baldo, “Simplified calculation of dipole energy transport in a multilayer stack using dyadic Green’s functions,” Optics Express, vol. 15, pp. 1762-1772, Feb. 2007.
- M. Segal, M.A. Baldo, R.J. Holmes, S.R. Forrest, and Z.G. Soos, “Excitonic singlet-triplet ratios in molecular and polymeric organic materials,” Phys. Rev. B, vol. 68, p. 075211, Aug 2003.